
皆様初めまして。ソフトウェアエンジニアの宇田川です。今回はモノグサ社内でボードゲームを真剣にやっている様子をお伝えしようと思います。
モノグサでは、「恐怖の古代寺院」というボードゲームが流行っています。
このゲーム内ではカードをランダムに配ることがあり、そのときのカード配分の発生確率を知っていると少し有利になる場面があります。
そこで、今回は、
特殊なカードM枚を含んだ合計N枚のカードをK人にランダムに同枚数ずつ配る場合、あるM枚の配分パターンが実際に起こる確率
をシミュレーションを用いて算出します。
次のような一場面をきっかけに分析をしてみることにしました。
(ゲームの詳細に踏み込んだ話になりますので、読み飛ばしていただいても構いません。)
ルール概要
ハンターチームとガーディアンチームに分かれて戦うチーム戦です。財宝カード数枚と罠カード数枚を含むカード山札をプレイヤーにランダムに配ります。配られたカードは自分だけが見ることができます。財宝カードを先にすべて見つけられればハンターの勝ちで、逆に罠カードを先にすべて見つけられればガーディアンの勝ちです。プレイヤーはゲーム中は自由に発言ができ、嘘を付いても良いので状況に応じて財宝や罠の数を偽ってくるプレイヤーがいます。
公式サイト
www.schmidtspiele.deTempel des Schreckens - 75046 - Schmidt Spiele
7人プレイの場合
役職は8枚のカードからランダムに引いて決まる。1枚は余り。
ハンター :4 ~ 5人 (期待値:35/8人)
ガーディアン:3 ~ 2人 (期待値:21/8人)
財宝カード :7枚
罠カード :2枚
空き部屋 :26枚
とあるゲームプレイ時の状況
プレイヤー人数7人でゲームをしました。
1ターン目にハンターの私の手元に財宝が2枚ありました。
全員に財宝の所持枚数を聞いたところ、 {0, 0, 0, 1, 2, 2, 3} という自己申告がありました。つまり、0枚所持が3人、1枚所持が1人、2枚所持が2人(うち1人は自分自身)、3枚所持が1人です。
ここで私はふと思いました。
「財宝は合計7枚で自分のところに2枚もあるのに、他に3枚持っている人が実際にいる確率は感覚的にはかなり低そう。ガーディアンが罠を持っていて嘘をついている気がする。3枚持っていると主張しているのがゲームが得意なCTOなので、きっと嘘だろう! そうに違いない!」
結果は、CTOはハンターであり正直に申告していたのですが、最後まで信じきれずに負けてしまいました。
「このような誤ちは繰り返さないようにしよう! 正しい確率を覚えておこう!」と考え、以下のシミュレーションの実行に至ったのでした。
シミュレーションで確率を算出
モンテカルロ・シミュレーションをしました。
数学的確率を計算可能ではありますが複雑な計算になると思われるため、今回はしていません。
試行回数は、それぞれ 10,000,000回 行いました。C++で実装しました。
特殊なカードが1種類の場合
特殊なカードM枚を含んだ合計N枚のカードをK人に均等に配る場合、あるM枚の配分パターンが実際に起こる確率
これを以下のような条件設定でシミュレーションした結果を表にまとめてみました。
(K, M, N)=(6, 5, 30), (6, 2, 30) の2通り
配分パターンは、以下の2パターンとします
P1:特定の1人が特殊なカードをQ枚所持している
P2:特殊なカードをQ枚所持している人が1人以上いる
特定の1人が特殊なカードをQ枚所持している確率表(P1)

特殊なカードをQ枚所持している人が1人以上いる確率表(P2)

目安ですが、どの値も95%信頼区間で誤差±0.1%以下です。
冒頭の自分の考えは、「自分が財宝を2枚持っているのに、他に3枚以上持っている人がいることなんて稀だ!」ということなので、自分の手札の情報を引いて
(K, M, N, P, Q)=(6, 5, 30, 2, 3 or 4 or 5)
を表から読み取って、足します。
発生確率は、約13.1%でした。
特殊なカードが2種類の場合
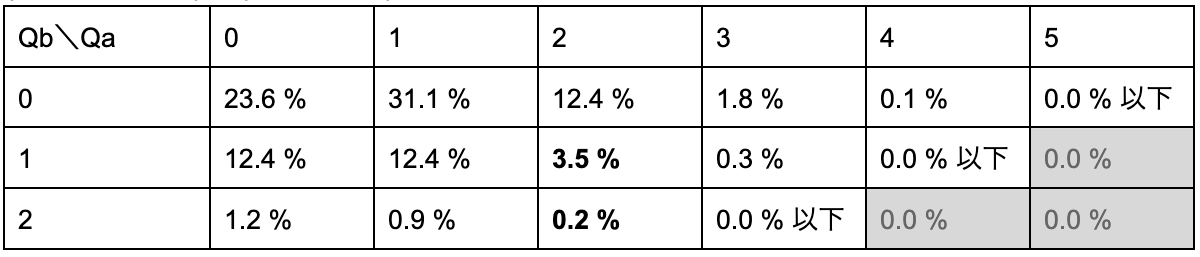
特殊なカードAをMa枚、特殊なカードBをMb枚を含む合計N枚のカードをK人にランダムに同枚数ずつ配る場合、ある特定の1人にAがQa枚、BがQb枚配られる確率
(K, Ma, Mb, N)=(6, 5, 2, 30)のときの上記の確率表(P1)
ゲームの状況の考察
ここからは冒頭のゲームにおける具体的な状況に即した私の考えを説明します。
この項目も、ゲームの詳細に踏み込んだ話になります。
さて、自分が財宝2枚所持しているとき自分以外に財宝3枚以上所持者がいる確率は、表によると 13.1% でした。
シミュレーションの確率は上記の通りですが、ゲームでは嘘を付く・付かないという2つの選択肢があります。
このゲームではハンターとガーディアンは自由に正直なことや嘘を言えますが、この記事では考察をシンプルにするためにハンターは常に正直なことを言う「正直者」、ガーディアンは特定の状況でのみ嘘をつく「嘘つき」という仮定を置きます。
そして、今回の分析では財宝3枚以上所持申告者が本当に3枚以上所持しているかを考察し、前述の表と数理的な近所計算を使って求めてみます。
ここで今後の説明のために起こる事象を以下のように定義します。

前の項目で求めた、自分が正直者で財宝を2枚所持しているとき自分以外に財宝3枚以上所持者がいる確率は、
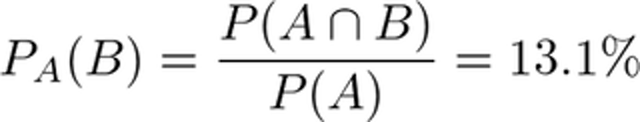
実際は、YやZのように嘘を付くケースがありますので、これらを用いると求める確率は以下の式になります。
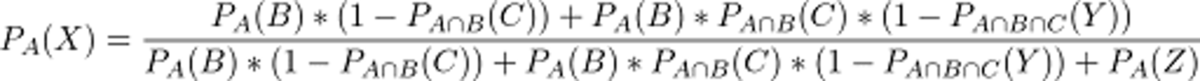
状況や戦術を単純化して、さらに以下の仮定を置きます。
財宝3枚以上所持の嘘つきは必ず財宝2枚以下だと嘘をつく
財宝2枚ちょうど所持かつ罠1枚以上所持の嘘つきだけが必ず財宝3枚以上所持と嘘をつく
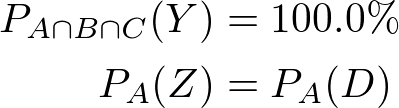
必要な値は表を参照して、以下のように近似計算をします。
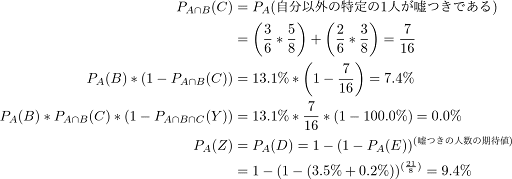
よって、求めたい確率は、
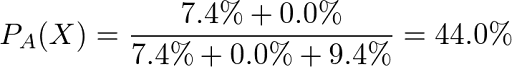
結果の解釈としては、「嘘つきであっても財宝3枚所持申告は珍しいことだから、申告を信じられるかは半々くらい」ということでしょう。
仮定で置いた条件が自分が考える戦術と少し異なる場合でも、今回の計算結果を元に確率を少し調整すれば良いので、実戦で使える数字だと思います。
最後に
いかがでしたでしょうか?
私は確率表を見て、配られたカードが偏ることは意外とあり得ると感じました。
今回のゲームは1ターン目の情報が少なく、他人の顔色や性格(メタ情報)を利用することが多いですが、上記のような確率の計算結果を知っておくと自分のバイアスを少し修正できるかもしれません。
また、このようなカードの配り方をするゲームは他にもたくさんありますので、この表を覚えておくとゲームを有利に進められることがあるかもしれません。
モノグサでは、いつでもボードゲームで遊ぶ余裕を持つという行動指針があり、職種の壁なく体現しています!
今後も楽しくボードゲームをしつつ、一緒に働く仲間を募集しています。
少しでも興味を持っていただけた方はぜひお話しましょう!
<付録>
少し簡略化したコードです。
using namespace std; #define REP(NAME, NUM) for (int NAME = 0; NAME < int(NUM); ++NAME) random_device rnd_device; mt19937 mt; enum CardType { Empty, Treasure, Trap, }; int rand(int begin, int end) { uniform_int_distribution dist(begin, end - 1); return dist(mt); } struct Card { int idx = 0; CardType type = Empty; }; struct Player { int idx = 0; vector<Card *> hands; }; vector<Card> generateCards( int num, const function<CardType(int)>& decideTypeFunc) { vector<Card> cards(num, Card()); REP(i, cards.size()) { auto& card = cards[i]; card.idx = i; card.type = decideTypeFunc(card.idx); } return cards; } vector<Player> generatePlayers(int num) { vector<Player> players(num, Player()); REP(i, players.size()) { auto& player = players[i]; player.idx = i; player.hands.clear(); } return players; } void dealCards(vector<Card>& cards, vector<Player>& players) { // init for (auto& player : players) player.hands.clear(); // shuffle vector<int> order(cards.size(), 0); REP(i, order.size()) order[i] = i; REP(i, order.size()) { int j = rand(i, order.size()); swap(order[i], order[j]); } // deal for (int c = 0, p = 0; c < int(cards.size()); ++c, p = (p + 1) % players.size()) players[p].hands.push_back(&cards[order[c]]); } int numInHands(const Player& player, CardType type) { auto cards = player.hands; int typeCount = 0; for (const auto* card : cards) if (card->type == type) ++typeCount; return typeCount; }; int main() { // ---------------- const int TRIAL_COUNT = 10000000; const int PLAYER_NUM = 6; // K const int CARD_NUM = 5 * PLAYER_NUM; // N const int TREASURE_NUM = 5; // Ma const int TRAP_NUM = 2; // Mb const int SEARCH_NUM = 3; // Q const function<CardType(int)> CARD_TYPE_FUNC = [](auto idx) { if (idx < TREASURE_NUM) return Treasure; else if (idx < TREASURE_NUM + TRAP_NUM) return Trap; return Empty; }; const function<double(vector<Player> &)> CHECK = [SEARCH_NUM](auto& players) -> double { // example P2 REP(playerIdx, players.size()) if (numInHands(players[playerIdx], Treasure) == SEARCH_NUM) return 1.0; return 0.0; }; // ---------------- mt.seed(rnd_device()); auto cards = generateCards(CARD_NUM, CARD_TYPE_FUNC); auto players = generatePlayers(PLAYER_NUM); double average = 0.0; REP(count, TRIAL_COUNT) { dealCards(cards, players); auto value = CHECK(players); average = (average * count + value) / (count + 1); } cout << fixed << setprecision(8) << "Average: " << average << endl; return 0; }