2023-04-06

AHC019 に参加してみた

ソフトウェアエンジニアの杉江（AtCoder ID: tsutaj）です。

2 年ほど前から、プログラミングコンテストサイト「AtCoder」でヒューリスティックコンテスト（通称：AHC）が開催されています。どんなコンテストなのか簡単に説明すると、最適解を出すことが難しい問題に対して、できるだけ良い解を出すプログラムを期間内に作成するコンテストです。

先日 MC Digital プログラミングコンテスト2023（AtCoder Heuristic Contest 019）に参加して、結果は 89 位（正の得点を得た 737 人中）でした。どんな解法になったのか書いていきます。

この記事を読んでヒューリスティックコンテストに興味が出ましたら、ぜひコンテストにも参加してみてください！

問題概要

atcoder.jp

三次元物体を正面から見たシルエット・右から見たシルエットが 2 組与えられます。 $1 \times 1 \times 1$ の立方体を面同士でくっつけてできるポリキューブ状のブロックの集合をひとつ決め、それらのブロックを使って正面・右シルエットが完全一致するようなポリキューブの配置を求めてください。同じブロックの集合を使って 2 組のシルエット両方について完全一致できる必要があります。

（ざっくり言うと）できるだけ大きく、できるだけ少ない数のブロックの組み合わせで実現できると高い評価が得られます。片方のシルエットの組でしか使われず、もう片方では使われないブロックが存在しても良いですが、そうするとスコアが減点されてしまいます。

自分の解法

一言で言うと「力まかせに答えを見つける」という解法で、条件を満たすまでランダムにポリキューブを決めて配置することを繰り返します。ですが、闇雲に探索をしても良いスコアにはならないため、いろいろ工夫しました。

配置するポリキューブのサイズを制限する

$N$ 個の立方体からなるポリキューブは何種類あるか考えてみます。以下の表は Wikipedia の記事から引用したものですが、 $N$ が大きくなると爆発的に増えるようです。（今回は鏡像を区別するので左側の列が参考になります）

このことから、サイズ 5 までのポリキューブに限定して探索することにしました。適当にはめていくだけで本当に解が作れるの？と思われるかもしれませんが、意外と作れます。

しかしこれに限定して探索しただけだと、当然ですが得られる解にはサイズ 5 までのポリキューブしか登場しません。より大きなポリキューブも欲しいので、シルエットの条件をある程度満たしたらポリキューブをマージしたり伸ばしたりすることで、より大きなポリキューブになるようにしました。その操作をしたあとに、解として正当な状態になっていれば OK です。

ちなみに、上位陣の解法を見ていると、ポリキューブの形状と位置を決めてから配置できるか試すのではなく、各シルエットについて適当に始点を決めて、始点から伸ばせるだけ伸ばしている方がちらほらいました。私は「この方針だったらブロックの大きさのバランスが取れないだろう」と思って捨ててしまいましたが、うまくやるとできるんですね。。。

条件を満たしたら、解を部分的に破壊する

最終日の前日まで、私の解法は「正当な解を求めることを繰り返す」ものでしたが、正当な解がひとつ得られたあと、それを完全に忘れてまっさらな状態でもう一度探索を始めていました。解が得られるまでに割と時間がかかることもあってこれでは非効率的です。

そこで、正当な解が得られたあとは部分的に破壊して、途中から再度探索するようにしました。ポリキューブのサイズが最も小さいもの（複数ある場合はどれか 1 つ）を選んで、それ自身とその周囲にあるものを消すことで部分的破壊をしました。サイズの小さいポリキューブを除去した状態からまた探索できるので、これを実装するだけで順位表上のスコアが約 1.25 倍になりました。

解を部分的に破壊しているため、状態の近傍（少し変化させた状態）を取っています。上位の解法を見ていると、ざっと見ただけでも他に以下のような近傍のとり方があるようです。とても勉強になりました。

ポリキューブの平行移動
セルの譲渡（一方で使用していた領域を、隣接している他方のポリキューブに譲る）
取り除いても解の条件を満たすようなセルの削除

高速化

探索がどれくらい回るのかは解法の性能に直結します。多く回れば回るほど良いです。そのため、どのコンテストでも高速化は重要になります。今回もたびたび高速化に迫られました。

私は Rust でコンテストに参加していますが、flamegraph でボトルネックを見つけるのをよくやります。処理時間全体に対して各処理がどれくらいの割合で行われているかがわかるので、幅の大きい部分を重点的に直していきました。

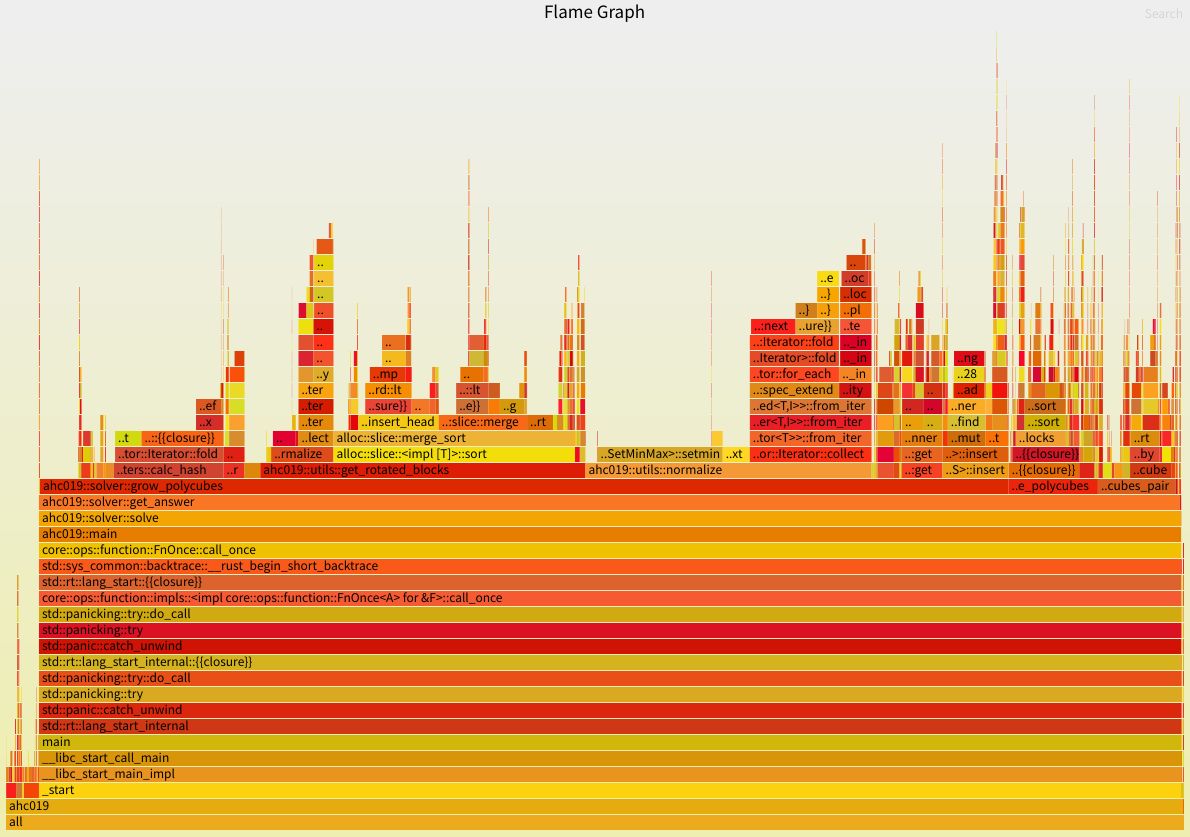
高速化にたびたび効いたのは Zobrist Hashing でした。各座標に乱数を事前に割り振っておき、ポリキューブ（の位置を正規化したもの）が占める座標に対応する乱数の XOR を取ることで、ポリキューブ同士が同型かどうか判定しました。Zobrist Hashing については以下の記事を参考にしました。

trap.jp

同型なポリキューブのペアについて、座標と回転方向のマッピングができればハッシュを使わなくても処理が出来るかとは思いますが、複数の方向で同型になる場合があったり、ペアの入れ替えをしたくなったりしてどうも納得いくものができず、結局ハッシュにずっと甘える形になりました。。。どこかで表現度を落としてでも高速化に振り切ってもよかったかもしれません。

解法まとめ

自分の解法を簡潔にまとめると次のようになります。やっていること自体はシンプルですが、実装はそこそこ大変でした。

最終提出へのリンク

焼きなまし法の適用

コンテスト後に「解を部分的破壊しているところは近傍選択っぽいし、焼きなまし法にできるのでは？」とふと思ったので、やってみました。

今までの解法は「常に解を採用し、それを部分的破壊して次の探索に進む」というもので、貪欲に解の生成を繰り返しているだけでした。これを次のように変えてみました。

解が良くなったら常に、解が悪くなったら確率的に採用したのち、それを部分的破壊して再開する。採用しない場合は最後に部分的破壊を行った状態から再開する。
不採用が一定回数続いた場合、何も置いていない状態から再度探索する。

こうすることで、手元で 1000 ケース回したときのスコア平均が 6% ほど改善しました。近傍を増やしたり、温度を調整したりするとさらに伸びるかもしれません。焼きなまし法にもっと慣れていきたいですね。

焼きなまし法を適用した提出へのリンク

さいごに

この問題の答えを人力で見つけるのはかなり大変だと思います（というか自分には無理です）。ですが、自分が書いたプログラムに任せればいい感じの答えが見つかります。自分の書いたプログラムで、自分には不可能なことが可能になる点が、ヒューリスティックコンテストの面白さのひとつだと感じています。

最終日の前日までスコアが思うように伸びず挫けそうにもなりましたが、粘り強く考えて最後にいい手法が思いつけてよかったです。とはいえまだまだ伸びしろは十分なので復習したいですね。

モノグサでは、記憶のプラットフォーム「Monoxer」を全人類に届けることを諦めない、粘り強いエンジニアを募集しています！！

careers.monoxer.com

2023-03-30

Monoxer Intern Report #11_日本語誤答生成の改善

インターンレポートアルゴリズム

自己紹介

モノグサのソフトウェアエンジニアインターンに参加した北村祐稀です。普段は大阪大学で情報科学教育の教材研究に取り組んでいます。

2023-03-15

正しい嘘解法入門

アルゴリズム競技プログラミング部

ソフトウェアエンジニアの大橋（AtCoder: amylase）です。

今回は競技プログラミングの話をします。それも、企業の技術ブログにありがちな “競技プログラミングが業務に役立った話” ではなく、純粋にコンテストに出た問題の話です。一見怪しく見える幾何の近似を正当化します。最後までお付き合いください。

問題

atcoder.jp

辺の長さが $A, B$ である長方形の中にできるだけ大きな正三角形を描くとき、その辺の長さを出力してください。

$1 \le A, B \le 1000$
答えと出力の絶対誤差または相対誤差が $10^{-9}$ 以下ならば正解

近似解

本問を解く上で重要な性質は「最大の正三角形は長方形と頂点を共有する」というものでした。今回これの解説はしませんが、公式解説が非常にきれいなので見てない人は今見てください。

この性質が成り立っているとき、共有する頂点で長さ $A$ の辺と三角形の近い辺がなす角を $\theta$ とすると、この問題の答えは共有する頂点から伸びる2辺のうち短いほうの長さ、すなわち

$\displaystyle{ \max_{0 \le \theta \le \frac{\pi}{6}} \min\left( \frac{A}{\cos\theta}, \frac{B}{\cos \left( \frac{\pi}{6} - \theta \right)} \right) }$

です。

ここで試したくなる嘘解法が「 $\theta$ を細かく刻んでたくさん試す」であり、実際に弊社の競プロ部員もこの解法で正解しています。部内で話題になったのが彼の「6000万分割ではWAになるが8000万分割ではACになる」という報告でした。これはたまたまなのでしょうか？　誤差を見積もってみましょう。

誤差評価

$A \lt B \cos{\frac{\pi}{6}}$ のときは簡単にわかるので、以下 $B \cos\frac{\pi}{6} \lt A \lt B$ とします。

$\displaystyle{ f(\theta) = \frac{A}{\cos{\theta}}, g(\theta) = \frac{B}{\cos{(\frac{\pi}{6} - \theta})} }$

とおくと、 $f$ が単調増加、 $g$ が単調減少なので、求める最大値は $f(\theta) = g(\theta)$ なるただ一つの $\theta = \theta_{\max}$ により与えられることがわかり、 $f(0) \gt g(0)$ かつ $f(\frac{\pi}{12}) \lt g(\frac{\pi}{12})$ なので、 $0 \lt \theta_{\max} \lt \frac{\pi}{12}$ であることがわかります。

$f, g$ のグラフを $\theta_{\max}$ の周辺で拡大すると次の図のようになります（ $f, g$ は直線で近似します）。角度を分割する戦略では、角度の分割幅を $\varepsilon$ とするとある角度 $\theta$ があって $\theta \le \theta_{\max} \le \theta + \varepsilon$ となるので、そこに着目すると図のような点の位置関係になります。

$f, g$ の微小変化を見積もります。 $\theta_{\max}$ の周辺での傾きは、 $f, g$ を微分してそれぞれ

$\displaystyle{ f'(\theta_{\max}) = \frac{A\sin(\theta_{\max})}{\cos^2(\theta_{\max})}, g'(\theta_{\max}) = -\frac{B\sin(\frac{\pi}{6} - \theta_{\max})}{\cos^2(\frac{\pi}{6} - \theta_{\max})} }$

とわかるので、 $f, g$ の微小変化はそれらの $\varepsilon$ 倍です。

解の絶対誤差が最大になるのは2つの近似解候補が等しいとき（図の点 $P, Q$ が同じ高さにある）で、この時の絶対誤差は2つの微小変化の調和平均の半分になります。調和平均を幾何平均で上から押さえて三角関数の計算をゴリゴリすると解の絶対誤差は

$\displaystyle{ \frac{ \varepsilon \sqrt{AB} \sin{\frac{\pi}{12}} }{ 2 \cos{\frac{\pi}{6}} } }$

で抑えられます。次の準備として、 $B \cos{\frac{\pi}{6}} \lt A$ を用いて $B$ を消去し、

$\displaystyle{ \frac{ \varepsilon A \sin{\frac{\pi}{12}} }{ 2 \cos^{\frac{3}{2}}{\frac{\pi}{6}} } }$

で抑えておきましょう。

解は少なくとも $(\sqrt{6} - \sqrt{2}) A$ （正方形の場合）より大きいので、絶対誤差の評価とあわせて相対誤差は

$\displaystyle{ \frac{\varepsilon \sin{\frac{\pi}{12}}}{2 (\sqrt{6} - \sqrt{2}) \cos^{\frac{3}{2}}{\frac{\pi}{6}}} }$

より小さくなります。

分割数を $d$ とおくと $\varepsilon = \frac{\pi}{6d}$ なので、分割数を具体的に決めることで以下のように相対誤差を評価できます。

6000万分割: $\lt 1.356 \times 10^{-9}$

8000万分割: $\lt 1.016 \times 10^{-9}$

残念ながら微妙に足りないですが*1、おそらく $\theta_{\max}$ が $\frac{\pi}{24}$ より大きいか小さいかで場合分けするなどして精密に評価すると $10^{-9}$ より小さいことがきちんといえるのではないかと思います。それかもう8200万分割で提出しましょう（相対誤差 $\lt 9.904 \times 10^{-10}$ ）。

いかがでしたか？

$f, g$ の交点が解であり $f - g$ が単調であるとわかったときに二分法を適用するのが競技プログラミングとしては最適ですが、コンテストに参加する者なら痛感しているように常に最適な解法を選択できるとは限りません。怪しい近似をするとき、嘘仮定を置くときに本稿を思い出して「もしかしたら証明できるかもしれないしな！」と自信を持って提出していただけると幸いです。

モノグサは、誤差評価を改善して8000万分割の正当性をきちんと言えるような腕力のある人材を募集しています！　一緒に働けたら最高ですが、証明だけでも大歓迎です。

careers.monoxer.com

*1:下書き段階では証明が誤っていて、8000万の時だけ制約を満たすようになっていました。悲しい……

2022-11-08

Monoxer Intern Report #10_音声読み上げに関する機能追加

インターンレポート

自己紹介

こんにちは、モノグサ株式会社でソフトウェアエンジニアのインターンとして働いていた大森です。この大森さんとは別の大森です。現在は東京大学大学院でコード並列化の研究をおこなっています。モノグサでは通年インターンとして昨年の10月ごろから勤務していてちょうど1年になります。この記事ではインターン中に取り組んだ課題やモノグサでの働き方について紹介したいと思います。