ソフトウェア上での数式表現と数式を操作するアルゴリズム

ソフトウエアエンジニアの深谷です。

今回はモノグサの中でも使われている数式表現に関して話したいと思います。

Monoxerの問題形式には数式という形式があり、この形式では一般の問題作成者が問題文や解答を数式を使って指定することができます。

この時、数式を問題作成に指定してもらうために、MathMLをフォーマットとして使っています。

モノグサの数式機能の詳細についてはこちらを参照してみてください。

今回はこのMathMLの簡単な紹介と、MathMLで動作するアルゴリズムをいくつか紹介します。

コンピュータ上で数式を表現するフォーマット
MathMLと木構造
参考文献

コンピュータ上で数式を表現するフォーマット

数式を文字列で表現するフォーマットとして、LaTeXやMathMLがあります。例えば、

$\frac{1}{k^{2}+1}$ のような数式を表現したいとしましょう。

LaTeXで書きたい場合は以下のように記述します。

\frac{1}{k^{2}+1}

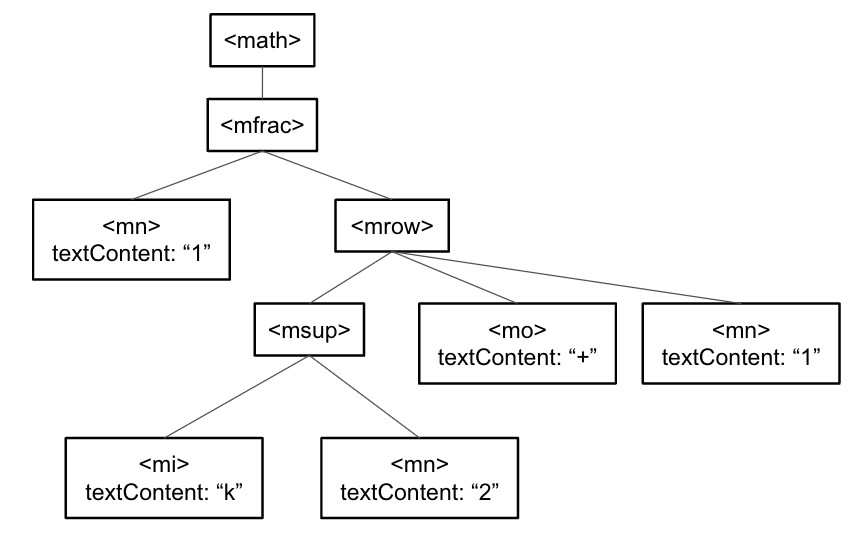
MathMLで書いた場合は以下のように記述します。（①）

<math xmlns='http://www.w3.org/1998/Math/MathML'>
  <mfrac>
    <mn> 1 </mn>
    <mrow>
      <msup>
        <mi> k </mi>
        <mn> 2 </mn>
      </msup>
      <mo> + </mo>
      <mn> 1 </mn>
    </mrow>
  </mfrac>
</math>

LaTeX表記の方が簡潔でわかりやすいと感じる人が多いのではないでしょうか？

LaTeXでは分数を\fracを使って表し、最初の要素が分子、二番目の要素が分母となります。

また、指数は^を使って表されます。

MathMLでは分数を<mfrac>を使って表し、<mn> 1 </mn>が分子、以降が分母となります。

（MathML仕様の詳細はこちら）

MathMLと木構造

MathMLは人間が読み解くにはあまり適していませんが、プログラムとしては扱いやすい構造を持っています。

MathMLはXMLの一種であり、XMLは根付きの木構造であるため MathMLもまた根付きの木構造 です。

①のMathMLをグラフとして表すと以下のようになります。

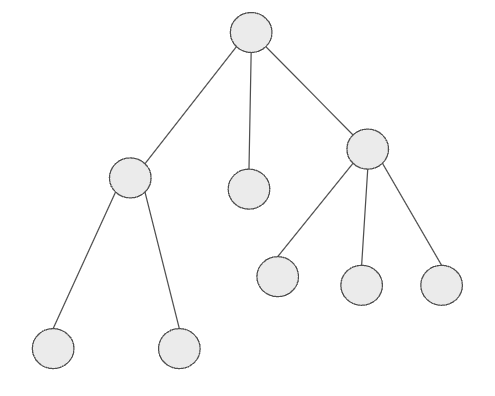
ここで木構造とは”連結でありサイクルを持たないグラフ”のことをいいます。

木構造のグラフの例

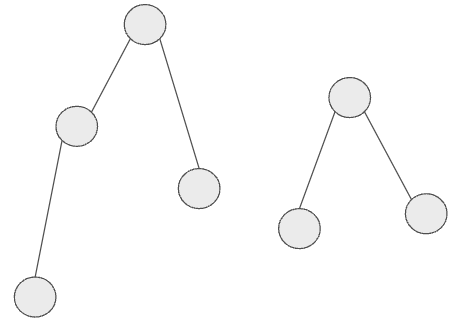
木構造でないグラフの例

連結ではないグラフ

サイクルを持っているグラフ

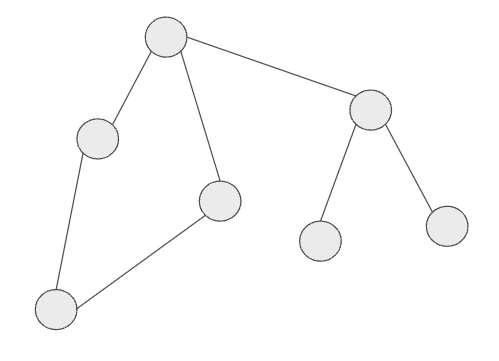
木構造は

頂点をN個とした時に辺がN-1本ある
任意の頂点間の最短路が常に一つに定まる

などの性質を持ちます。

競技プログラミングをしている方などには馴染み深いデータ構造なのではないでしょうか？ DFS、BFS、LCA、木DPのような木構造上で動作するアルゴリズムも豊富で、面白い題材です。私は木構造とその問題が大好きなので、数式機能開発の日々に生きがいを感じています（？）。

（余談：日々再帰を書いて鍛えられているおかげか、先日のAtCoder Beginner Contestのこの問題もACできました！）

この記事ではMathMLを題材に木構造を扱うアルゴリズムを紹介したいと思います。

MathMLのバリデーション

Monoxerではユーザーが入力したMathMLを正解として登録することができますが、ユーザーが作成するがゆえに、MathMLとして不正なものが入力として入ることがあります。

そこで、ユーザーが入力したMathMLが不正かどうかを判定する必要があります。

ここでMathMLに不正な入力としては

XMLとして不正である（タグが閉じていないなど）
MathMLに存在しないタグが使われている
MathMLのタグの個別ルールに違反している

といったものがあります。 MathMLのタグの個別ルールにはどんなものがあるかというと、例えば分数を表す<mfrac>というタグは、子要素をちょうど二つ含む必要があります。

また数値を表す<mn>というタグではtextContentをもち、その内容は数値として解釈できる文字列である必要があります。

詳細はこちらを参照してみてください。

MathMLが不正でないか確認するためには以下のようなDFSを書くと良いでしょう。

from typing import *

class MathElement:  # 抽象クラス
    def __init__(self, children: List["MathElement"]):
        self.children = children
        
    def isValid(self) -> bool:
        return False # 呼ばれないはず

class MathRoot(MathElement):  # MathMLの根, validであるためには子要素が全てvalidである必要がある
     def isValid(self) -> bool:
        return all([child for child in self.children])

class MathMn(MathElement):  # 数値の要素, validであるためには子要素が数値として解釈できる文字列である必要があります。
    def __init__(self, textContent: str):
        self.textContent = textContent

    def isValid(self) -> bool:
        try:
            float(self.textContent)
        except ValueError:
            return False
        return True

    def asInt(self) -> int:
        return int(self.textContent)

class MathMfrac(MathElement):  # 分数, validであるためには子要素数がちょうど二つであり、いずれもvalidである必要がある。
     def isValid(self) -> bool:
        return len(self.children) == 2 and all([isinstance(child, MathElement) and child.isValid() for child in self.children])

ここで、MathMLの各タグに対応するクラスは各言語のxmlパーサを使って得るものとします。

MathRootはパースされたMathMLの根であり、MathRoot.isValid()を呼ぶことで再帰的に不正な箇所がないかサーチされます。

MathML上での乱択

次に数式選択問題の誤答を生成することを考えてみます。

誤答生成はMonoxerの重要な機能の一つですが、数式でもサポートされています。

複雑な数式をスマホで入力するのに比べて、タップ一つで回答を送信できる選択問題はユーザーの負荷が小さいため選択問題が選ばれることがあります。

数式の選択肢を手動で指定することもできますが、自動化によって問題作成の負荷を小さくすることができます。

例えば

${2x}^2 + 4x + 5$ という数式から、

${2x}^2 + 2x + 5$ や ${2x}^2 + 4x - 5$ というような誤答を生成します。

誤答生成の際には、元のMathMLの要素から一部を変更することを考えます。

この時には乱択というアルゴリズムを使いますが、この時に木上での要素をランダムに選択する必要があります。例えば、数値要素（MathMn）をランダムに選択するためには、DFSで全ての数値要素に訪問し行きがけ順でのインデックスを振った後にインデックスを乱数で指定してやれば良いです。

実装としては以下のようになります。

import random
from typing import *


def dfsExtractMn(elem: MathElement, extractedMns: List[MathMn]):
    for child in elem.children():
        if isinstance(child, "MathMn"):
            extractedMns.append(child)
        else:
            dfsExtractMn(child, extractedMns)


extractedMns = []
dfsExtractMn(root, extractedMns)
# ランダムに一つmnを選択する
choosedMn = extractedMns[random.randrange(0, len(extractedMns))]

約分されていない分数のサーチ

さて、このようにして誤答を選んだ時、不自然な誤答が出ることがあります。

3 / 4という正解に対して、 6 / 4という誤答が出てしまったとします。

すると、「6 / 4は3 / 2に約分できるのでどうやら誤答っぽいぞ？」と回答者に勘づかれる可能性があります。

ここで整数によって約分可能である分数をサーチすることを考えてみましょう。

いくつか実装方法はありますが、 LCA（最近共通祖先）という概念を使うことで、簡単に判定することできます。 LCAとは根付き木において、二頂点の共通の祖先で、最も近いところにある頂点のことをいいます。*1

例えば以下の図において、頂点Aと頂点BのLCAは頂点Cです。

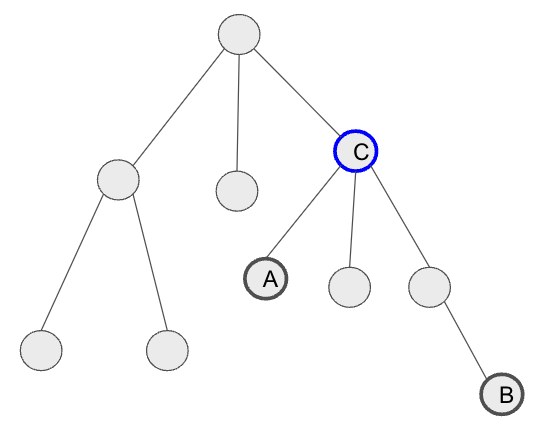
LCAの算出方法については他のブログや参考文献に譲ります。

LCAが得られれば、全ての頂点のペアに対してLCAが分数を表す<mfrac>であり、かつ最大公約数が1より大きい場合には約分可能な分数が存在するということになります。

import math
from typing import *

def findReducibleFraction(mns: List[MathMn]) -> Optional[MathFrac]:
    for a in range(mns):
        for b in range(mns):
            if isinstance(child, "MathFrac") and math.gcd(a.asInt(), b.asInt()) > 1:
                return lca(a, b)
    return None  # 見つからなかった

ここで、 $\frac{2x + 1}{4}$ のように一部の分子の項だけが約分できるときは約分可能と見なしたくないが、 $\frac{2x + 4}{4}$ ではのように全ての分子が約分できる時に約分可能と見なしたいというようなこともあり得ます。その場合にはmfracごとに全ての子要素の最大公約数が1より大きくないかを見るといいでしょう。実装は以下のようになります。

import math
from functools import reduce
from typing import *

def findReducibleFraction(root: MathElement) -> Optional[MathFrac]:
    for child in root.children:
        if isinstance(child, "MathFrac"):
            mnNumbers = [elem.asInt() for elem in child.children if isinstance(child, "MathMn")]
            g = reduce(lambda x, y: math.gcd(x, y), mnNumbers)  # 分母分子全ての数の最大公約数
            if g > 1:
                return child  # 約分できる分数の発見
        else:
            result = findReducibleFraction(child)
            if result is not None:
                return result
    return None  # 見つからなかった

いかがでしたでしょうか？モノグサでは高度木構造人材（？）を募集しております！！！

参考文献

プログラミングコンテストチャレンジブック[第二版]　秋葉拓哉, 岩田陽一, 北川宜稔 (著)